Logistic Regression

1. Giới thiệu

Hôm nay chúng ta cùng đi qua một trong những thuật toán phổ biến nhất trong nhóm thuật toán về Supervised Learning, cụ thể hơn là Classification được gọi là Logistic Regression.

Cụ thể hơn nữa Logistic Regression được sử dụng trong các bài toán Binary Classification

Nội dung

• Hàm giả thuyết
• Loss Function
• Gradient Descent
• Dự đoán kết quả

2. Hàm giả thuyết

Các bạn còn nhớ bài đầu tiên mình có nói để xác định được model chúng ta cần biết: Dạng của model hay còn được gọi là hàm giải thuyết và các parameters $w$ của hàm đó.

Nguồn: https://en.wikipedia.org/wiki/Sigmoid_function

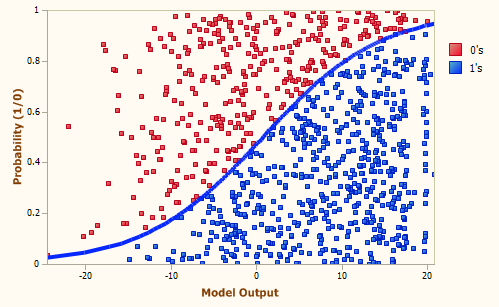
Hàm giả thuyết của Logistic Regression được gọi là sigmoid

$$\sigma(x) = \frac{1}{1 + e^{wx}}$$

Mình muốn nhắc các bạn là $wx$ là nhân giữa 2 vector chứ không phải nhân giữa 2 số nhé. Vì trong Machine Learning mọi thứ nên được biểu vector hóa hoặc biểu diễn dưới dạng ma trân, để tăng tốc độ tính toán.

$x = [x_1, x_2,...,x_n]$, $w = [w_0, w_1, w_2, ...w_n]$ với $n$ là số feature. $w_0$ được gọi là bias.

Đặc điểm của hàm sigmoid là:

• Giá trị đầu ra nằm trong đoạn $[0, 1]$. Đó là lý do tại sao nó có tên là Regression nhưng lại được sử dụng trong bài toán Classification, vì đầu ra của nó là các giá trị liên tục, trải đều trên tập số thực và nằm trong đoạn giá trị cho phép
• Liên tục, có đạo hàm tại mọi điểm

3. Loss Function

Các bạn còn nhớ bài trước mình đã giới thiệu một số Loss Function thường gặp không? Trong bài viết đó mình có nhắc đến Cross Entropy. Thuật toán Logistic Regression sử dụng Cross Entropy để làm Loss Function. Còn giải thích tại sao thì trong bài viết đó mình có giải thích rồi nên bài viết này mình không giải thích lại nữa.

$$L = \frac{-\sum_{i=1}^{N}(y_{i}log(\hat{y_i}) + (1 - y_i)log(1 - \hat{y_i})}{N}$$

Với $y_i$ là label của điểm dữ liệu thứ $i$ và $\hat{y_i}$ là giá trị mà model dự đoán của với đầu vào là vector feature $x$ của điểm dữ liệu thứ $i$ (đây chính là output của sigmoid ứng với parameter $w$)

4. Gradient Descent

Có hàm giả thuyết(tức là có dạng của model) bây giờ chúng ta cần tìm parameter $w$ sao cho Loss Function đạt giá trị nhỏ nhất. Lúc này thứ ta nghĩ tơi là sử dụng Gradient Descent, mình đã trình bày ở bài viết trước các bạn có thể xem lại

Kết thúc quá trình cập nhật ta được parameter $w$ tối ưu nhất

5. Dự đoán kết quả

Sau tất cả chúng ta có được model cuối cùng, bây giờ giả sử chúng ta truyền vào hàm sigmoid tức là model một vector $x_{test}$ nào đó. Output của model sẽ là giá trị nằm trong đoạn $[0, 1]$ bây giờ chúng ta cần biết với giá trị này thì nó ứng với class 0 hay 1 vì đây là bài toán Binary Classification mà. Lúc này ta chỉ cần so sánh với một ngưỡng nào đó nếu lớn hơn ngưỡng thì nó thuộc class 1, ngược lại thì thuộc class 0. Tất nhiên là ngưỡng cũng sẽ nằm trong khoảng $[0, 1]$ thường được chọn là $0.5$

Bản chất của Logistic Regression là tìm bounary phân tách dữ liệu

Nguồn: https://miro.medium.com/max/499/1*fQNbPl3NY4antjKJPeuxwA.png

Như vậy trên đây mình đã trình bày cho các bạn về Logistic Regression, đây cũng có thể được xem như một mạng Neural Network sơ khai. Mình xin dừng bài viết tại đây nếu có thắc mắc gì các bạn vui lòng để lại comment phía dưới. Xin cảm ơn