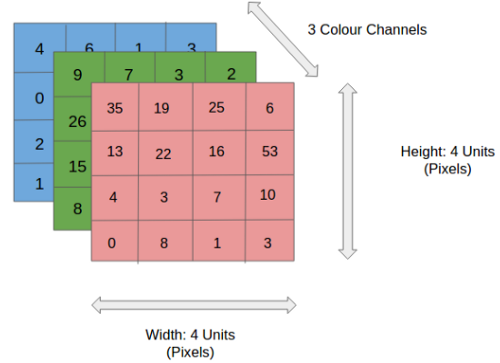
1. Giới thiệu
Hôm nay chúng ta tiếp tục đi sang phần tiếp theo về xử lý ảnh cơ bản
Nội dung
- Phép tích chập convolutional
- Các phép toán khác trên ảnh
2. Phép tích chập convolutional
Trước tiên chúng ta cùng đi qua ví dụ dưới đây để hiểu rõ phép tích chập là gì.
 Nguồn: https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53
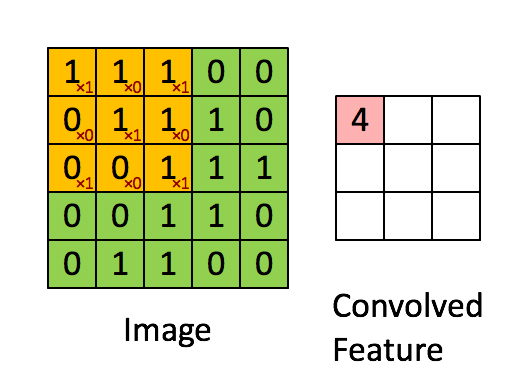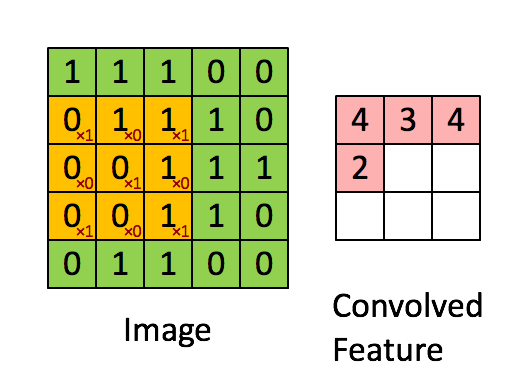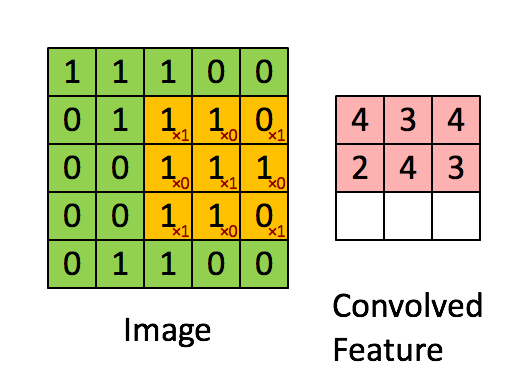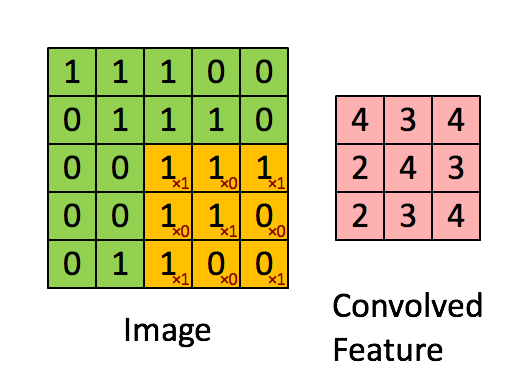
Nguồn: https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53Các bạn quan sát ma trận màu vàng được gọi là kernel hay filter
$$K = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 1\\ \end{bmatrix}$$
Còn ma trận màu xanh là ảnh
$$I = \begin{bmatrix} 1 & 1 & 1 & 0 & 0\\ 0 & 1 & 1 & 1 & 0\\ 0 & 0 & 1 & 1 & 1\\ 0 & 0 & 1 & 1 & 0\\ 0 & 1 & 1 & 0 & 0\\ \end{bmatrix}$$
Ma trận tích chập của Kernel K và ảnh I ký hiệu $C=K⊗I$ (là ma trận màu hồng ở trên) được thực hiện bằng việc trượt ma trận kernel K lên ảnh I từ trên xuống dưới từ trái sang phải. Tại mỗi vị trí của kernel trên ảnh ta nhân các phần tử tương ứng xong cộng lại tất cả.
Ví dụ vị trí đầu tiên trên ma trận C ta có phép tính sau: $$C_{11}=1*1+0*1+1*1+0*0+1*1+0*1+1*0+0*0+1*1=4$$
$$C_{12}=1*1+0*1+1*0+0*1+1*1+0*1+1*0+0*1+1*1=3$$
Tính toán tương tự với $C_{13}, C_{21}, C_{22}, C_{23}, C_{31}, C_{32}, C_{33}$
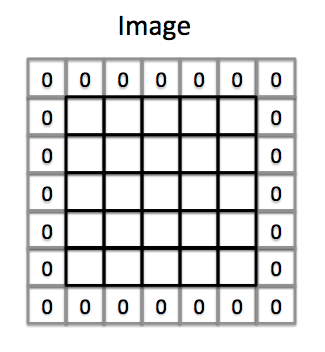
Gọi $P$ là padding của ảnh, nếu $P=1$ ta được ảnh với padding như hình dưới đây
Lúc này kernel sẽ bắt đầu tự vị trí padding di chuyển từ trái sang phải, trên xuống dưới.
Gọi S là bước nhảy hay thường được gọi stride
Quan sát hình ta thấy nếu stride bằng 1 thì mỗi lần kernel dịch chuyển sang một cột hoặc một hàng(hình trên). Còn nếu stride bằng 2 thì mỗi lần kernel sẽ dịch chuyển 2 cột hoặc 2 hàng(hình dưới) sau đó mới tiến hành sử dụng các phép toán tích chập
Gọi kích thước của ảnh là $w_I*h_I$, padding là P, stride là S, kích thước kernel là $w_K*h_K$ khi đó kích thước output sau phép tích chập là $w_C*h_C$ được tính toán như sau
$$w_C = \frac{w_I - w_K + 2P}{S}+1$$
$$h_C = \frac{h_I - h_K + 2P}{S}+1$$
Từ công thức trên ta thấy việc stride lớn sẽ làm giảm kích thước output, padding lớn sẽ làm tăng kích thước output
Các bạn có thể quan sát trực quan hơn về phép tích chập tại đây
Việc sử dụng convolutional giúp chúng ta trích xuất được các đặc trưng của ảnh như: cạnh, góc hoặc làm nét làm mờ ảnh. Tác dụng của convolutional như thế nào phụ thuộc vào filter ta sử dụng
3. Các phép toán khác trên ảnh
Biến đổi hình học
Đây là phép biến đổi hình ảnh từ dạng này sang dạng khác thông qua việc làm thay đổi phương, chiều, góc của ảnh ban đầu mà không làm thay đổi nội dung ban đầu của ảnh. Về cơ bản phép biến đổi này là sử dụng một ma trận dịch chuyển (translation matrix) $M$. Với mỗi điểm có tọa độ $x, y$ trên ảnh gốc thông qua phép biến đổi $T$ ta sẽ được ảnh trong không gian mới sau dịch chuyển là $T(x, y)$
$$T(x, y) = M \begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix} \begin{bmatrix} x*a_{11} & y*a_{12}\\ x*a_{21} & y*a_{22} \end{bmatrix}$$
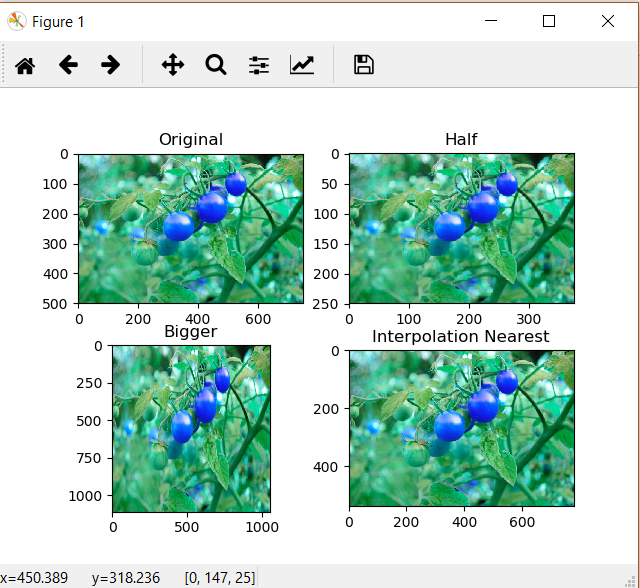
Thay đổi kích thước ảnh là thay đổi kích thước dài, rộng của ảnh mà không làm thay đổi tính chất song song của các đoạn thẳng trên ảnh gốc so với các trục tọa độ X và Y. Ta có ma trận dịch chuyển có dạng
$$M=\begin{bmatrix} a_{1} & 0\\ 0 & a_{2} \end{bmatrix}$$
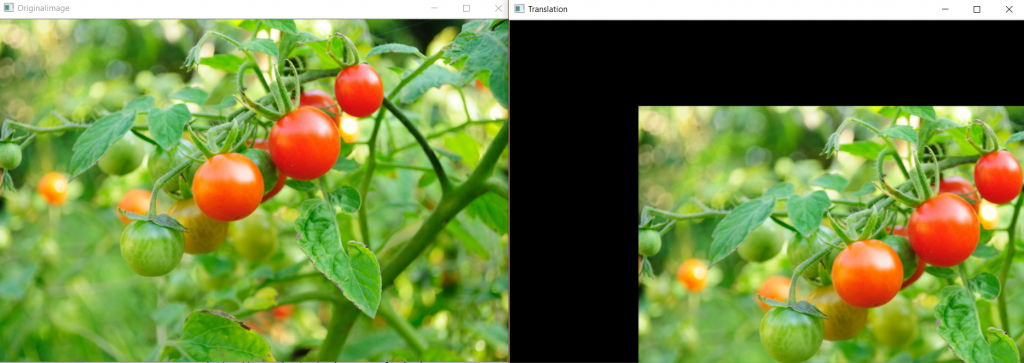
Dịch chuyển ảnh là việc dịch chuyển ảnh đến các vị trí khác nhau ví dụ tới các góc trái, phải, ở giữa, bên trên, bên dưới. Phép dịch chuyển sẽ giữ nguyên tính chất song song của các đoạn thẳng sau dịch chuyển đối với các trục X hoặc Y nếu trước dịch chuyển chúng cũng song song với một trong hai trục này. Ma trận dịch chuyển có dạng
$$M=\begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y \end{bmatrix}$$
Với $t_x, t_y$ là các giá trị dịch chuyển theo trục x và y
Xoay ảnh là quay một bức ảnh theo một góc xác định quanh một điểm nào đó. Ma trận dịch chuyển có dạng
$$M=\begin{bmatrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{bmatrix}$$
 Nguồn: https://cppsecrets.com/users/204211510411798104971091085153504964103109971051084699111109/C00-OpenCV-to-rotate-an-image.php
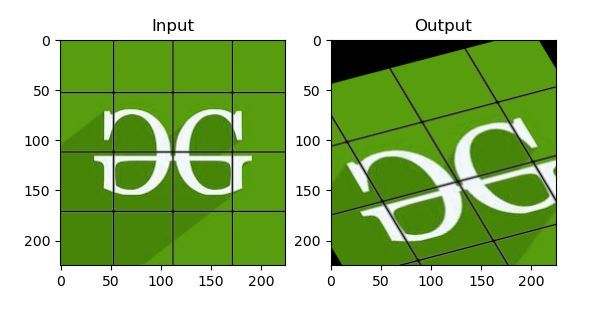
Nguồn: https://cppsecrets.com/users/204211510411798104971091085153504964103109971051084699111109/C00-OpenCV-to-rotate-an-image.phpBiến đổi affine, toàn bộ các đường thẳng song song trong bức ảnh gốc giữ nguyên tính chất song song ở ảnh đầu ra. Để tìm ma trận dịch chuyển, chúng ta cần xác định ra 3 điểm từ ảnh đầu vào và tọa độ tương ứng của chúng trong hình ảnh đầu ra. Được tính như hình dưới đây:
Như hình trên với 3 điểm đầu vào ($x, y$) và 3 điểm đầu ra ($x', y'$) ta giải được hệ phương trình để tìm A và B. Sau đó áp dùng A, B cho các điểm khác để được ảnh mới
Biến đổi phối cảnh (perspective) Để biến đổi phối cảnh thì chúng ta cần một ma trận biến đổi 3x3. Đường thẳng sẽ giữ nguyên là đường thẳng sau biến đổi. Để tìm ra ma trận biến đổi này, chúng ta cần tìm ra 4 điểm trong ảnh đầu vào tương ứng với các điểm trong ảnh đầu ra. Trong số 4 điểm này, không có bất kì 3 điểm nào thẳng hàng. Cách tính ma trận dịch chuyển như biến đổi affine
Làm mờ ảnh sử dụng phép tích chập convolutional như mình đã giới thiệu ở trên với kernel là ma trận $5*5$
$$K = \frac{1}{5}\begin{bmatrix} 1 & 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 & 1\\ \end{bmatrix}$$Ngoài ra còn có một số bộ lọc khác như Gaussian, Median. Các bạn có thể tìm hiểu thêm
Trên đây là một số kiến thức cơ bản về xử lý ảnh. Nếu có thắc mắc gì vui lòng để lại comment phía dưới. Xin cảm ơn